FRICCIÓN Y SUS LEYES

La fuerza de fricción o la fuerza de rozamiento es la fuerza que existe entre dos superficies en contacto, que se opone al movimiento relativo entre ambas superficies (fuerza de fricción dinámica) o a la fuerza que se opone al inicio del deslizamiento (fuerza de fricción estática). Se genera debido a las imperfecciones, mayormente microscópicas, entre las superficies en contacto. 
Estas imperfecciones hacen que la fuerza perpendicular R entre ambas superficies no lo sea perfectamente, sino que forme un ángulo con la normal N(el ángulo de rozamiento). Por tanto, la fuerza resultante se compone de la fuerza normal N (perpendicular a las superficies en contacto) y de la fuerza de rozamiento F, paralela a las superficies en contacto.

Fricción estática: no se inicia el movimiento si la fuerza tangencial aplicada T hace que el ángulo sea menor a φ₀ (no supera a Fr).

Fricción estática

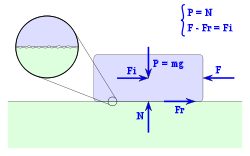
Es la fuerza que se opone al inicio del deslizamiento . Sobre un cuerpo en reposo al que se aplica una fuerza horizontal F, intervienen cuatro fuerzas:

F: la fuerza aplicada.

F_r: la fuerza de rozamiento entre la superficie de apoyo y el cuerpo, y que se opone al deslizamiento.

P: el peso del propio cuerpo

N: la fuerza normal.

Dado que el cuerpo está en reposo la fuerza aplicada y la fuerza de rozamiento son iguales, y el peso del cuerpo y la normal:

${\displaystyle {\begin{cases}P=N\\F=F_{r}\end{cases}}}$

Se sabe que el peso del cuerpo P es el producto de su masa por la aceleración de la gravedad (g), y que la fuerza de rozamiento es el coeficiente estático por la normal:

${\displaystyle P=N=mg\,}$

${\displaystyle F=F_{r}=\mu _{e}N\,}$

esto es:

${\displaystyle F=F_{r}=\mu _{e}mg\,}$

La fuerza horizontal F máxima que se puede aplicar a un cuerpo en reposo es igual al coeficiente de rozamiento estático por su masa y por la aceleración de la gravedad.

Fricción dinámica

Dado un cuerpo en movimiento sobre una superficie horizontal, deben considerarse las siguientes fuerzas:

F_a: la fuerza aplicada.

F_r: la fuerza de rozamiento entre la superficie de apoyo y el cuerpo, y que se opone al deslizamiento.

P: el peso del propio cuerpo, igual a su masa por la aceleración de la gravedad.

N: la fuerza normal, que la superficie hace sobre el cuerpo sosteniéndolo.

Como equilibrio dinámico, se puede establecer que:

${\displaystyle {\begin{cases}P=N\\F=F_{a}-F_{r}\end{cases}}}$

Sabiendo que:

${\displaystyle P=N=mg\,}$

${\displaystyle F_{r}=\mu _{d}N\,}$

${\displaystyle F=ma\,}$

prescindiendo de los signos para tener en cuenta solo las magnitudes, se puede reescribir la segunda ecuación de equilibrio dinámico como:

${\displaystyle \mathbf {F} _{a}=\mu _{d}m\mathbf {g} +m\mathbf {a} ,\quad \Rightarrow \quad \mathbf {a} ={\frac {\mathbf {F} _{a}}{m}}-\mu _{d}\mathbf {g} }$

Es decir, la fuerza de empuje aplicada sobre el cuerpo ${\displaystyle \mathbf {F} _{a}}$ es igual a la fuerza resultante ${\displaystyle \mathbf {F} }$ menos la fuerza de rozamiento ${\displaystyle \mathbf {F} _{r}}$ que el cuerpo opone a ser acelerado. De esa misma expresión se deduce que la aceleración ${\displaystyle \mathbf {a} }$ que sufre el cuerpo, al aplicarle una fuerza Fa mayor que la fuerza de rozamiento Fr con la superficie sobre la que se apoya.

EJEMPLO PROBLEMA DE FUERZA DE FRICCIÓN

Sobre una caja de 1200 g de masa situado sobre en una mesa horizontal se aplica una fuerza de 15 N en la dirección del plano. Calcula la fuerza de rozamiento (fuerza de fricción) si:

a)  La caja adquiere una aceleración igual a 2,5 m/s2.
b)  La caja se mueve con velocidad constante. 

Datos

m = 1200 g = 1.2 Kg

F = 15 N

a = 2.5 m/s2
FR= ?

Resolución

Si aplicamos las ecuaciones de la segunda ley de Newton o principio fundamental de un cuerpo sobre un plano horizontal, obtenemos que:

F−FR=m⋅a ⇒FR=F−m⋅a ⇒FR=15 N−1.2 Kg ⋅ 2.5 m/s2 ⇒FR=12 N

Cuestión b)

Si tiene velocidad constante quiere decir que en este caso la aceleración de la caja es a = 0 m/s2, por tanto:

F−FR=m⋅a ⇒FR=F−m⋅a ⇒FR=15 N−1.2 Kg ⋅ 0 m/s2 ⇒FR=15 N